有限元(Finite Element,FE)是一种工程分析方法,它通过将复杂的结构或物理现象离散化为许多小的元素来进行数值计算和模拟。每个元素都是由简单的几何形状构成,如三角形或四边形,它们之间通过节点连接在一起。通过对每个元素进行分析和计算,可以得到整个结构或物理现象的行为和性能。
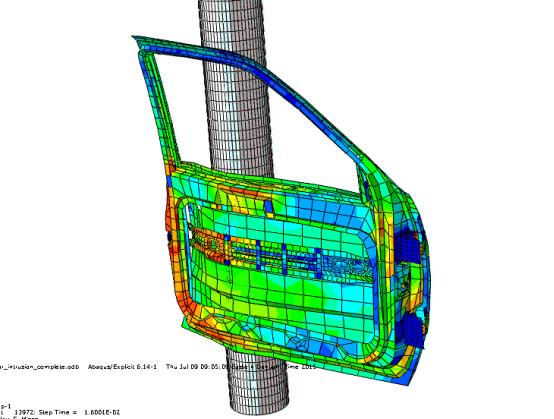
有限元方法最初是由Richard Courant于1943年提出的,它最初被应用于固体力学领域。随着计算机技术的发展,有限元方法得到了广泛应用,不仅可以用于固体力学,还可以用于热传导、流体力学、电磁学等领域。
有限元仿真是利用有限元方法进行数值计算和模拟的过程。它可以通过对结构或物理现象进行离散化,将其分解为许多小的元素,并在每个元素上进行数值计算和模拟。有限元仿真可以帮助工程师和设计师更好地了解结构或物理现象的行为和性能,从而进行优化设计和改进。
有限元仿真通常包括以下步骤:

1.建立有限元模型:将结构或物理现象离散化为许多小的元素,并在每个元素上定义材料特性和边界条件。
2.网格划分:将有限元模型划分为许多小的单元,每个单元都由几何形状和节点组成。
3.求解:在每个单元上进行数值计算和模拟,并通过节点将单元连接在一起,得到整个结构或物理现象的行为和性能。
4.后处理:对仿真结果进行分析和处理,以便更好地理解结构或物理现象的行为和性能。

有限元仿真是一种非常有用的工程分析方法,它可以帮助工程师和设计师更好地了解结构或物理现象的行为和性能,从而进行优化设计和改进。在实际工程项目中,有限元仿真已经成为不可或缺的工具之一。