什么是计算流体动力学（CFD）？

什么是计算流体动力学 (CFD)?

计算流体动力学（CFD）是使用计算机根据质量、动量和能量守恒的 governing 方程来预测液体和气体流动的科学。流体无处不在，以无数种方式维持我们的生活。你声带的振动在空气中产生压力波，使言语成为可能，同时也能听到所说的话。没有流体，你的网球的上旋将变得毫无意义，你的飞机也不会产生任何升力。通过CFD，我们可以分析、理解和预测构成我们世界几乎每个部分的流体。 

 

计算流体动力学示例 

CFD用于需要预测流体流动和热传递，或了解流体流动对产品或系统的影响的地方。CFD分析流体流动的不同特性，如温度、压力、速度和密度，并可应用于各个行业的广泛工程问题，包括：

 

航空航天与国防：计算流体动力学（CFD）使得能够模拟飞机周围的气流，以预测升力和阻力，这被称为外部流体动力学。这对于公司优化飞机设计以提高性能和减少燃料使用非常重要。CFD还可以模拟飞机内部的复杂系统，例如客舱空气循环，以预测空气质量。主要应用包括机载电子设备冷却、航空光学、外部流体动力学、客舱暖通空调和推进系统。

 

 

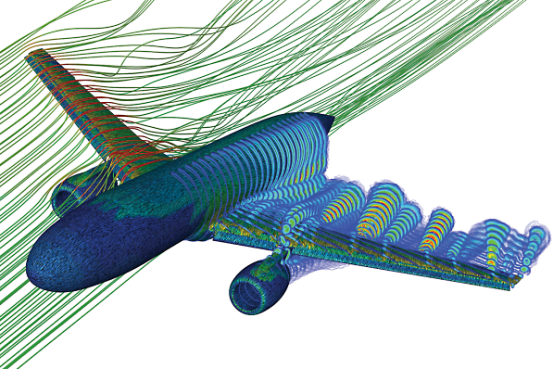
ANSYS Fluent对商用飞机外部空气动力学研究的模拟。

 

汽车： 在 电动汽车中，电动机和电池电化学在机械、化学和电气工程之间创造了复杂的交叉点，CFD 使我们能够在多物理系统中进行详细的热研究。这可以帮助工程师预测电动机的冷却效率，并减少可能导致火灾的电池热失控。主要应用包括变速箱润滑、自主传感器、声学、外部空气动力学、电池建模和电动机冷却。

 

 

使用 Ansys Fluent GPU 解算器求解的驱动器模型

 

新能源： 作为脱碳的推动者，氢气是一种创造更清洁星球的宝贵燃料。CFD使我们能够模拟整个氢价值链——从生产到储存、运输和消费。CFD可以进行探索性研究，以了解氢气和其他替代燃料如何在传统发动机中使用，并确定替代燃料选项的有效性。主要应用包括PEM电解、氢气生产、运输、储存和消费以及燃料电池的应用。

 

 

在Ansys Fluent中进行的燃烧研究

 

医疗保健： 在生物医学领域，CFD可以分析人体内的流体流动，例如血液通过循环系统和空气通过呼吸系统的流动。它还可以用于加速医疗设备的开发并评估新药的潜在疗效。主要应用包括心血管流动、呼吸系统、生物制药。

 

计算流体动力学如何运作

有许多不同的方法来在计算机上解决流体流动问题。在开始之前，你需要确定你将在高层面上使用什么方法，即解决什么控制方程。这个选择将缩小可用的计算方法。假设选择了连续体方法（这相当常见），基本上有3个步骤。 

 

首先，识别流体流动域（要计算的连续区域），通常由计算机辅助设计（CAD）模型表示。然后，应用网格将域分割成定义明确的单元格。最后，计算机在每个单元格内求解 governing 流体方程的离散版本。在高性能计算（HPC）的背景下，一个可选的步骤是将不同的单元格组分配给不同的计算机以进行并行处理。 

 

1. 确定需要解决的流体流动域

 

2. 将域离散化为所需的网格大小和网格间距

 

2. 将处理器分配到不同的区域，并应用适当的微积分方程

 

 

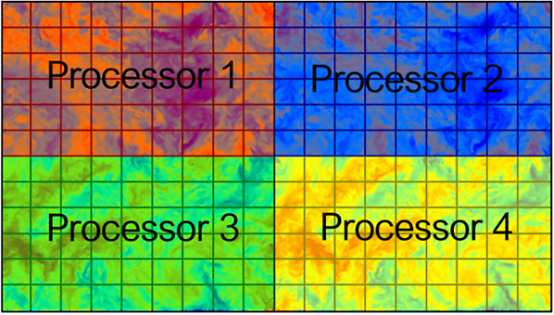
流体流动建模的挑战

流体流动的复杂性使得在计算机上模拟它本质上是困难的。多物理场相互作用、非线性和非定常性是一些使流体分析如此具有挑战性的复杂性。

 

多物理场交互： 流体通常不会单独流动：它们在结构内、通过和周围流动。想象一下风中的树木在移动。当树移动时，它改变了风，风也改变了树。流体与结构相互作用的这种耦合问题需要多物理场建模方法。

 

Ansys CFD 软件，例如 Fluent 和 LS-Dyna，可以解决这种流体-结构相互作用问题（有时与结构力学求解器耦合，例如 Ansys Mechanical）。即使在单独考虑流体的情况下，许多实际场景也涉及多种流体（例如气泡在水中上升）和/或流体化学成分通过反应发生变化（例如飞机发动机内的燃烧流或汽车电池中的化学反应）。Ansys Fluent 特别适合于建模这些情况。

 

非线性： 在流体动力学中，这 governing物理方程的性质意味着流体与自身相互作用。大多数工程上有意义的流动本质上是湍流。湍流是流体动力学中非线性的一个例子，因为湍流会影响其他量，如传热和动量，这些量反过来又会影响湍流。我们所说的湍流（是的，就像飞机上船长谈论的那样），是指流动是随机的、混乱的和非确定性的。

 

这种随机性就是计算流体动力学中“计算”一词的关键所在。由于非线性和湍流，这些方程无法用铅笔和纸来解决。必须在计算机上进行（除非是一些低维的简单层流）。即便如此，CFD 问题的答案也不是一个解——它是在将大量微积分转换为代数后计算机计算出的解。

不稳定性： 湍流的一个固有特征是不稳定性。这意味着在空间中的任何固定点的流动参数会随时间变化。如果这种不稳定性是显著的（例如，您的汽车在高速公路上行驶），高精度的模拟需要时间解析的解，这大大增加了成本。

 

广泛存在的湍流现象困扰着科学家和工程师们数十年。它非常复杂，以至于获得诺贝尔奖的理论物理学家理查德·费曼称其为“经典物理学中最重要的未解决问题”。虽然计算流体动力学（CFD）从数学上没有解决湍流问题，但它允许工程师在设计中考虑湍流的影响。 

 

计算流体动力学的历史

计算流体动力学的研究始于20世纪初，当时首次开发了用于解决流体流动的数学模型。随着计算机在20世纪中叶的出现，该领域迅速发展，得益于其计算速度和能够模拟越来越复杂的问题的能力。 

 

早期发展（1900年代-1940年代）：

用于流体流动的基本 governing方程，即纳维-斯托克斯方程，是经过推导的。这些方程为理解流体行为提供了理论框架。   

 

计算机出现（1950年代-1960年代）： 

这一转折点使得CFD能够以高速度进行复杂计算，并得到以前被认为无法解决的流体流动问题的答案。 

 

数值方法（1960年代-1970年代）： 

应用数值方法使研究人员能够将域划分为更小单元的网格，以求解每个单元内的流体特性。这使得可以分析更复杂的几何形状和边界条件。 

 

高性能计算 (HPC) (2000年代-现在): 

随着 高性能计算（HPC）的进步，运行更大、更复杂的计算流体动力学（CFD）模型并在更短的时间内完成成为可能。HPC的巨量处理能力使工程师能够在复杂的过程中进行极其庞大的计算，例如分析飞行中的整架飞机。 

 

计算流体动力学的 governing方程

许多人对流体运动的直观感受并不强烈，因为流体的运动方式与固体物体非常不同。如果你把一个球扔到房间的另一端，它不会改变形状或质量。你无法以相同的方式“扔”空气。计算流体动力学（CFD）的 governing equations 帮助我们补偿流体的任意形状和不可预测的特性。 

 

纳维-斯托克斯方程以克劳德-路易·纳维和乔治·加布里埃尔·斯托克斯的名字命名，用于描述流体的运动。这些方程在19世纪中叶发展起来，是理解流体动力学的基本方程，用于模拟各种流体流动，例如机翼周围的气流和发动机中的燃油流动。它们被认为是模拟流体行为的主要控制方程，并基于质量、动量和能量的守恒方程。  

 

1. 质量守恒：连续方程

该方程表明，除非有质量流入或流出，否则给定体积的流体的质量必须保持恒定：

 

 

 

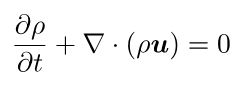
其中 ⍴ 是流体密度， t 是时间， u 是速度矢量，∇ 是梯度运算符。

 

2. 动量守恒：牛顿第二定律

动量方程表明，流体体积内动量的变化率等于作用在其上的所有力的总和，包括压力和重力。对于具有恒定粘度的不可压缩流体，我们可以写成：

 

 

 

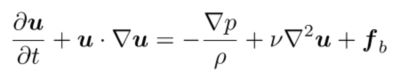
其中 p 是静压，v 是粘性，b 是体力（通常是重力）。

 

3. 能量守恒：热力学第一定律

能量方程表明，流体的总能量的变化必须等于添加到系统或从系统移除的能量（例如，通过导热或对流热传递）。

 

 

 

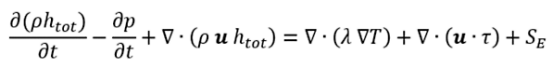
其中 htot 是总焓，λ 是导热系数，T 是温度，SE 是外部能量来源。项 ∇ ∙ ( u ∙ t ) 是粘性功项，代表由于粘性应力所做的功

 

计算流体动力学的进展

计算流体动力学（CFD）的潜力仅受计算硬件性能的限制。随着硬件和软件的进步，科学计算从CPU转移到GPU成为可能，包括应用多个GPU进行CFD模拟，这将带来速度和精度的巨大飞跃。完全原生的多GPU实现将进一步加速CFD模拟，推动新的性能水平，降低硬件成本，并降低功耗。