有限元分析是工程领域中常用的数值分析方法,它可以用来模拟和分析结构、零部件或系统的行为和性能。有限元分析通常包括几个基本步骤,下面我们将逐步介绍有限元分析的步骤及其具体内容。
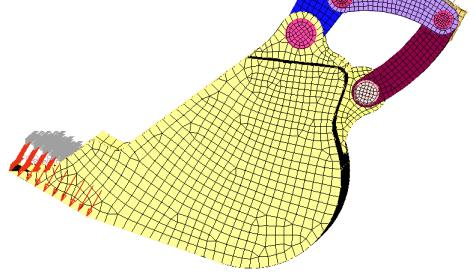
1. 问题定义:有限元分析的第一步是明确定义需要分析的问题,包括对结构或物理现象的要求、分析的目的和范围等。在这一阶段,需要收集和整理相关的设计参数、材料性质、荷载情况等信息,为后续的分析做好准备。
2. 几何建模:在进行有限元分析之前,需要对结构或物体的几何形状进行建模。这个几何模型可以是二维的,比如平面结构的截面图,也可以是三维的,比如实际零部件的三维模型。几何建模的准确性对有限元分析结果有重要影响,因此需要尽可能地符合实际结构的形状和尺寸。
3. 网格划分:有限元分析将结构或物理现象离散化为许多小的单元,这就需要进行网格划分来表示这些单元。网格划分的精细程度和质量对有限元分析的准确性和效率有重要影响,因此需要根据结构的几何形状和复杂程度来选择合适的网格划分方法。
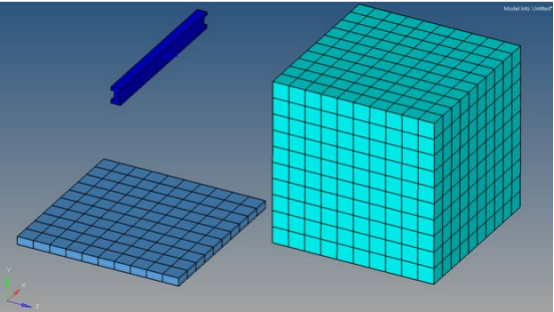
4. 材料属性分配:在有限元分析中,需要对材料的力学性质进行描述和分配。不同的材料具有不同的力学性质,比如弹性模量、屈服强度、断裂韧性等。因此,需要为每个单元分配合适的材料属性,以便进行有限元分析。
5. 载荷和约束条件施加:在有限元分析中,需要对结构施加相应的载荷和约束条件,以模拟实际工作状态。这包括力、压力、温度等载荷的施加,以及固定支撑、约束、边界固定等约束条件的施加。
6. 求解方程:一旦建立了有限元模型并施加了载荷和约束条件,就可以进行方程的求解。有限元分析通常涉及大量的代数方程,这些方程需要通过数值方法进行求解,得到结构或系统的响应和行为。
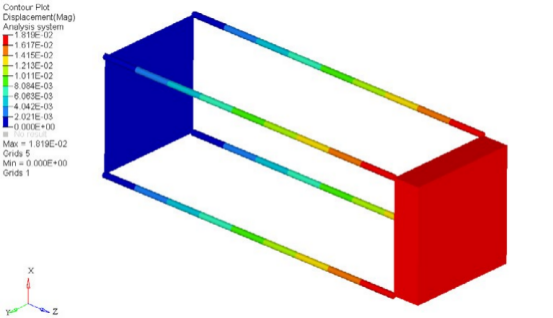
7. 结果评定:最后,需要对有限元分析的结果进行评定和分析。这包括对结构的位移、应力、应变等物理量的分析,以及对分析结果的准确性和可靠性进行评估。
总的来说,有限元分析的步骤包括问题定义、几何建模、网格划分、材料属性分配、载荷和约束条件施加、方程求解以及结果评定。这些步骤相互关联,需要有条不紊地进行,才能得到准确、可靠的分析结果,为工程设计和优化提供有力的支持。